ML

SVM

https://docs.opencv.org/4.5.0/d1/d73/tutorial_introduction_to_svm.html

https://opencv24-python-tutorials.readthedocs.io/en/latest/py_tutorials/py_ml/py_svm/py_svm_basics/py_svm_basics.html#svm-understanding

https://learnopencv.com/support-vector-machines-svm/

https://opencv24-python-tutorials.readthedocs.io/en/latest/py_tutorials/py_ml/py_svm/py_svm_opencv/py_svm_opencv.html

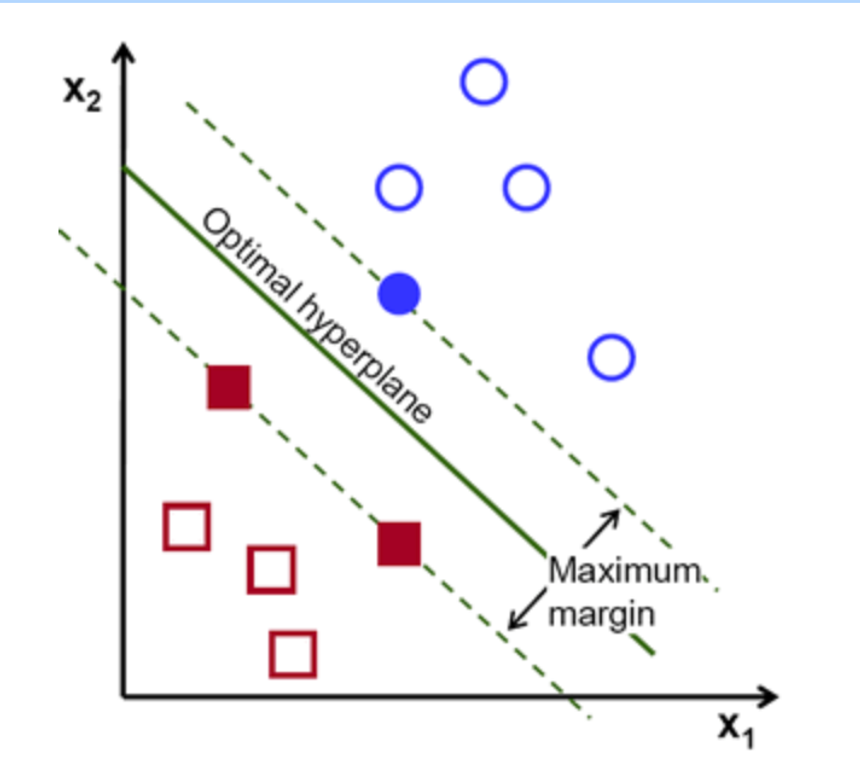
Definition of a hyperplane: f(x)=β0+βTxf(x)=\beta_0+\beta ^Txf(x)=β0​+βTx﻿​

Canonical hyperplane: by convention, among all the possible, we choose  ∣β0+βTx∣=1|\beta_0+\beta^Tx|=1∣β0​+βTx∣=1﻿, where xxx﻿ represent the training image closest to the hyperplane

Distance between a point and hyperplane: distance=β0+βTx∣∣β∣∣=1∣∣β∣∣distance=\frac{\beta_0+\beta^T x}{||\beta||}=\frac{1}{||\beta||}distance=∣∣β∣∣β0​+βTx​=∣∣β∣∣1​﻿​

The margin M is twice the distance to the closest example: M=2∣∣M∣∣M=\frac{2}{||M||}M=∣∣M∣∣2​﻿​

Finally, maximizing M is minimizing L(β)L(\beta)L(β)﻿ with some constraints to correctly classify all training examples

minβ,β0(L(β))=12∣∣β∣∣2min_{\beta,\beta_0}(L(\beta))=\frac{1}{2}||\beta||^2minβ,β0​​(L(β))=21​∣∣β∣∣2﻿ 

subject to

yi(βTxi+β0)2>1y_i(\beta^Tx_i+\beta_0)^2>1yi​(βTxi​+β0​)2>1﻿​

this is a Lagrangian optimization problem

full script

Python

Copy

labels = np.array([1, -1, -1, -1])
trainingData = np.matrix([[501, 10], [255, 10], [501, 255], [10, 501]], dtype=np.float32)
# train
svm = cv.ml.SVM_create()
svm.setType(cv.ml.SVM_C_SVC)
svm.setKernel(cv.ml.SVM_LINEAR)
svm.setTermCriteria((cv.TERM_CRITERIA_MAX_ITER, 100, 1e-6))

svm.train(trainingData, cv.ml.ROW_SAMPLE, labels)
# Data for visual representation
width = 512
height = 512
image = np.zeros((height, width, 3), dtype=np.uint8)

green = (0,255,0)
blue = (255,0,0)
for i in range(height):
for j in range(width):
        sampleMat = np.matrix([[j,i]], dtype=np.float32)
        response = svm.predict(sampleMat)[1]
if response == 1:
            image[i,j] = green
        elif response == -1:
            image[i,j] = blue

thickness = 2
sv = svm.getUncompressedSupportVectors()
for i in range(sv.shape[0]):
    cv.circle(image, (sv[i,0], sv[i,1]), 6, (128, 128, 128), thickness)

Non Linear SVM

The training data can be rarely separated using an hyperplane

Chance is more for a non-linear separable data in lower-dimensional space to become linear separable in higher-dimensional space.

In general, it is possible to map points in a d-dimensional space to some D-dimensional space to check the possibility of linear separability

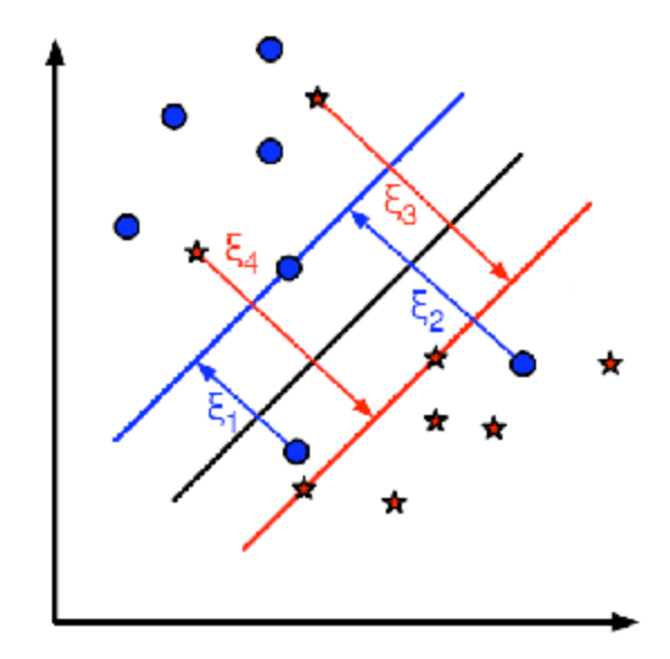
The new model has to include both the old requirement of finding the hyperplane that gives the biggest margin and the new one of generalizing the training data correctly by not allowing too many classification errors.

For example, one could think of minimizing the same quantity plus a constant times the number of misclassification errors in the training data

min∣∣β∣∣2+C(misclassification  error)min||\beta||^2+C(misclassification\;error)min∣∣β∣∣2+C(misclassificationerror)﻿​

A better solution will take into account the distance of the misclassified samples to their correct decision regions

min∣∣β∣∣2+C(distance  of  misclassified  samples  to  their  correct  regions)min||\beta||^2+C(distance\; of\; misclassified\; samples\; to\; their\; correct\; regions)min∣∣β∣∣2+C(distanceofmisclassifiedsamplestotheircorrectregions)﻿​

minβ,β0L(β)=∣∣β∣∣2+C∑iξimin_{\beta, \beta_0}L(\beta)=||\beta||^2+C\sum_i \xi_iminβ,β0​​L(β)=∣∣β∣∣2+C∑i​ξi​﻿​

subject to

yi(βTxi+β0)>1−ξiy_i(\beta^Tx_i+\beta_0)>1-\xi_iyi​(βTxi​+β0​)>1−ξi​﻿ and ξi>0\xi_i>0ξi​>0﻿​

Choose C

Large values give solutions with less classification errors but smaller margin

Small values of C give solutions focusing more on the hyperplane, without much importance for classification errors, so wider margin

Implementation

Python

Copy

svm = cv.ml.SVM_create()
svm.setType(cv.ml.SVM_C_SVC)
svm.setC(0.1) # new
svm.setKernel(cv.ml.SVM_LINEAR)
svm.setTermCriteria((cv.TERM_CRITERIA_MAX_ITER, int(1e7), 1e-6))

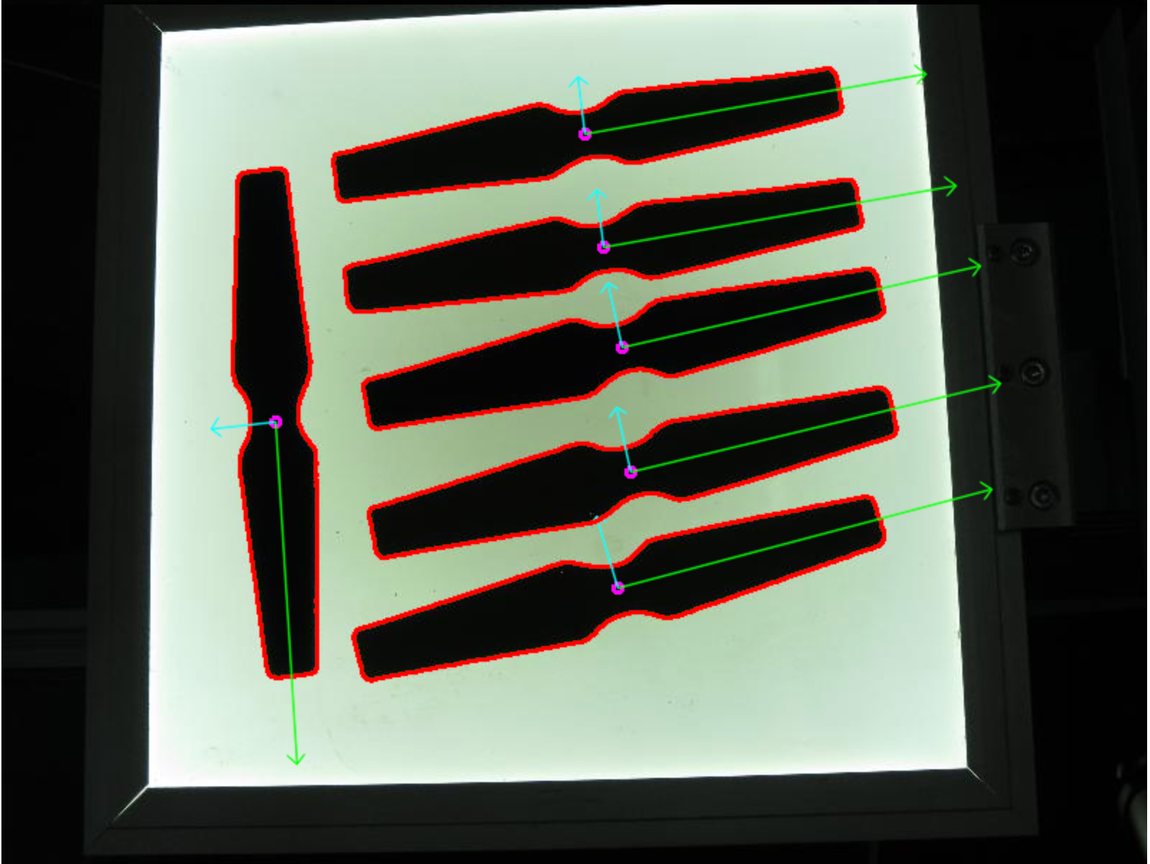
PCA

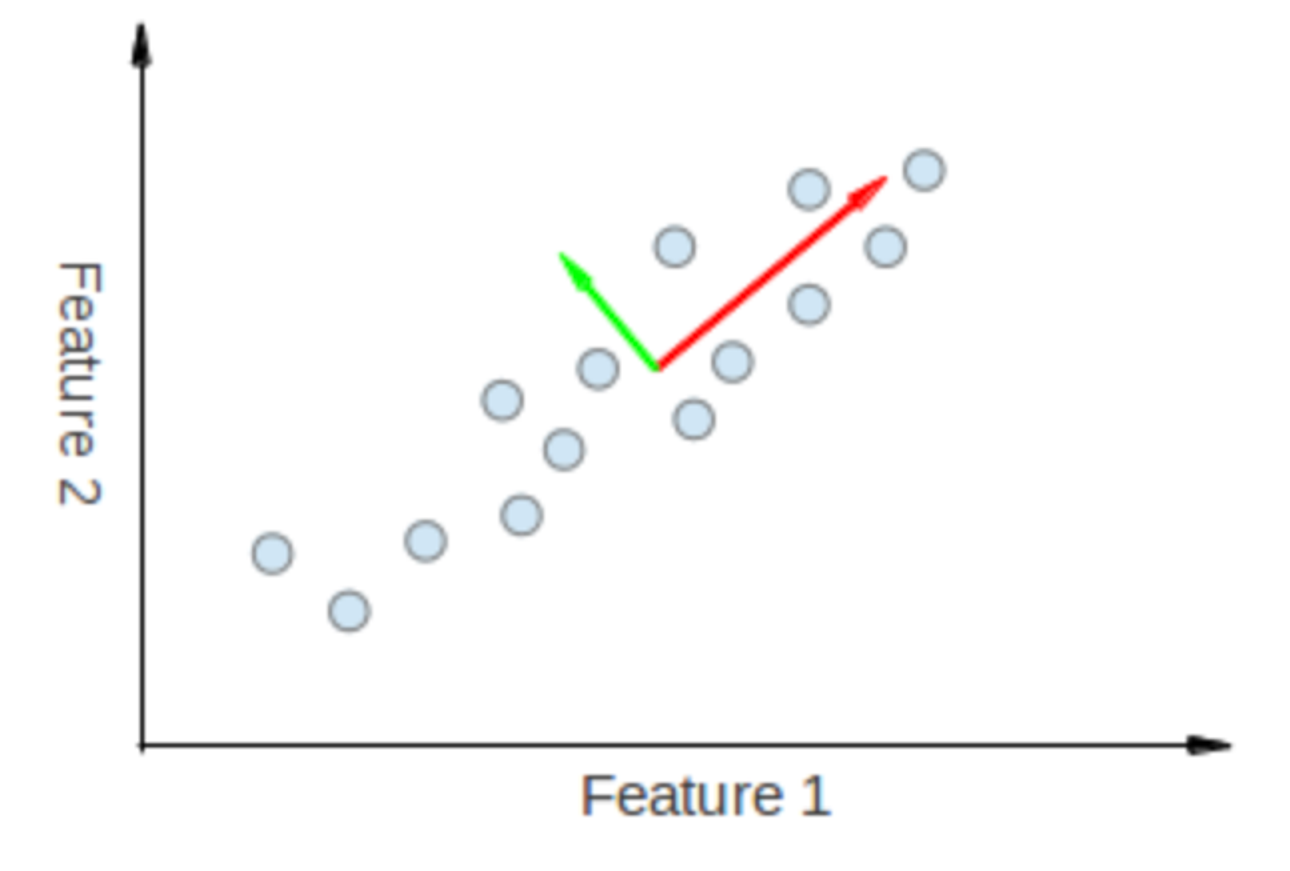
https://docs.opencv.org/4.5.0/d1/dee/tutorial_introduction_to_pca.html

eigenvectors

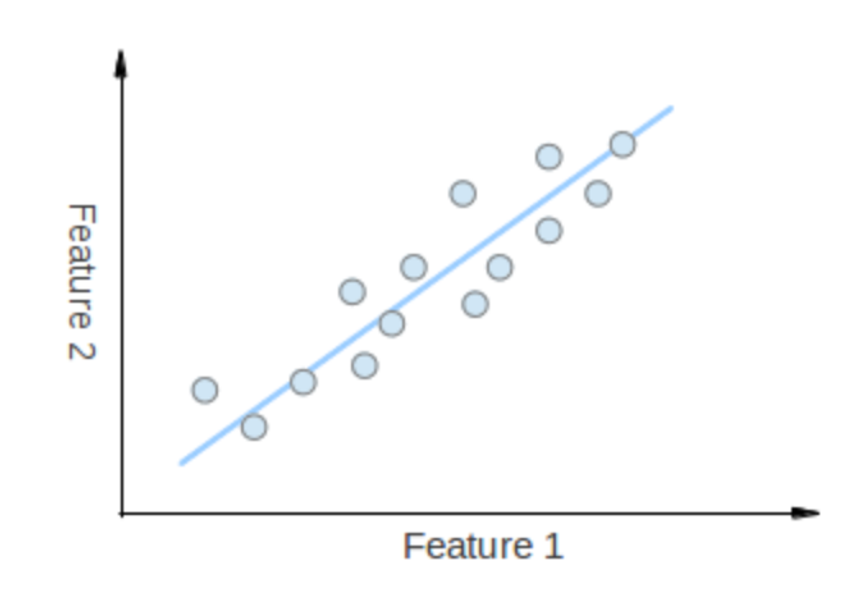
The points vary the most along the blue line, more than they vary along the Feature 1 or Feature 2 axes, so we'll be better off with that dimension only

We want to turn dataset XXX﻿ into a small dimension one YYY﻿​

Karhunen-Loève transform: Y=KLT{X}Y = \mathbb{KLT}\{X\}Y=KLT{X}﻿​

Algorithm

Compute empirical mean for every dimension

u[j]=1n∑inX[i,j]u[j]=\frac{1}{n}\sum_i^nX[i,j]u[j]=n1​∑in​X[i,j]﻿, with uuu﻿ vector of size (p, 1)

Compute deviation from mean

B=X−huTB=X-hu^TB=X−huT﻿ with h=[1,...,1]h = [1, ..., 1]h=[1,...,1]﻿, of size (n, 1)

Find the covariant matrix of size (p, p)

C=B∗.Bn−1C=\frac{B^*.B}{n-1}C=n−1B∗.B​﻿, where B∗B^*B∗﻿ is the conjugate transpose of BBB﻿​

If B consists only of real number, it is just the regular transpose.

SVD decomposition of the covariant matrix to find eigenvalues and eigenvectors

V−1CV=DV^{-1}CV=DV−1CV=D﻿​

With D=diag(λ1,...,λp)D=diag(\lambda_1,...,\lambda_p)D=diag(λ1​,...,λp​)﻿, with λi\lambda _iλi​﻿ being the i-th eigenvalues of C

VVV﻿ are eigenvectors, come in pairs with eigenvalues

full script

Python

Copy

from __future__ import print_function
from __future__ import division
import cv2 as cv
import numpy as np
import argparse
from math import atan2, cos, sin, sqrt, pi


def drawAxis(img, p_, q_, colour, scale):
    p = list(p_)
    q = list(q_)
    
    angle = atan2(p[1] - q[1], p[0] - q[0]) # angle in radians
    hypotenuse = sqrt((p[1] - q[1]) * (p[1] - q[1]) + (p[0] - q[0]) * (p[0] - q[0]))
# Here we lengthen the arrow by a factor of scale
    q[0] = p[0] - scale * hypotenuse * cos(angle)
    q[1] = p[1] - scale * hypotenuse * sin(angle)
    cv.line(img, (int(p[0]), int(p[1])), (int(q[0]), int(q[1])), colour, 1, cv.LINE_AA)
# create the arrow hooks
    p[0] = q[0] + 9 * cos(angle + pi / 4)
    p[1] = q[1] + 9 * sin(angle + pi / 4)
    cv.line(img, (int(p[0]), int(p[1])), (int(q[0]), int(q[1])), colour, 1, cv.LINE_AA)
    p[0] = q[0] + 9 * cos(angle - pi / 4)
    p[1] = q[1] + 9 * sin(angle - pi / 4)
    cv.line(img, (int(p[0]), int(p[1])), (int(q[0]), int(q[1])), colour, 1, cv.LINE_AA)
def getOrientation(pts, img):
    
    sz = len(pts)
    data_pts = np.empty((sz, 2), dtype=np.float64)
for i in range(data_pts.shape[0]):
        data_pts[i,0] = pts[i,0,0]
        data_pts[i,1] = pts[i,0,1]
# Perform PCA analysis
    mean = np.empty((0))
    mean, eigenvectors, eigenvalues = cv.PCACompute2(data_pts, mean)
# Store the center of the object
    cntr = (int(mean[0,0]), int(mean[0,1]))
    cv.circle(img, cntr, 3, (255, 0, 255), 2)
    p1 = (cntr[0] + 0.02 * eigenvectors[0,0] * eigenvalues[0,0], cntr[1] + 0.02 * eigenvectors[0,1] * eigenvalues[0,0])
    p2 = (cntr[0] - 0.02 * eigenvectors[1,0] * eigenvalues[1,0], cntr[1] - 0.02 * eigenvectors[1,1] * eigenvalues[1,0])
    
		drawAxis(img, cntr, p1, (0, 255, 0), 1)
    drawAxis(img, cntr, p2, (255, 255, 0), 5)

    angle = atan2(eigenvectors[0,1], eigenvectors[0,0]) # orientation in radians
return angle


parser = argparse.ArgumentParser(description='Code for Introduction to Principal Component Analysis (PCA) tutorial.\
                                              This program demonstrates how to use OpenCV PCA to extract the orientation of an object.')
parser.add_argument('--input', help='Path to input image.', default='pca_test1.jpg')
args = parser.parse_args()
src = cv.imread(cv.samples.findFile(args.input))
# Check if image is loaded successfully
if src is None:
print('Could not open or find the image: ', args.input)
    exit(0)
cv.imshow('src', src)
# Convert image to grayscale
gray = cv.cvtColor(src, cv.COLOR_BGR2GRAY)
# Convert image to binary
_, bw = cv.threshold(gray, 50, 255, cv.THRESH_BINARY | cv.THRESH_OTSU)
contours, _ = cv.findContours(bw, cv.RETR_LIST, cv.CHAIN_APPROX_NONE)
for i, c in enumerate(contours):
# Calculate the area of each contour
    area = cv.contourArea(c)
# Ignore contours that are too small or too large
if area < 1e2 or 1e5 < area:
continue
# Draw each contour only for visualisation purposes
    cv.drawContours(src, contours, i, (0, 0, 255), 2)
# Find the orientation of each shape
    getOrientation(c, src)

cv.imshow('output', src)
cv.waitKey()

Kmeans

Basic intuition

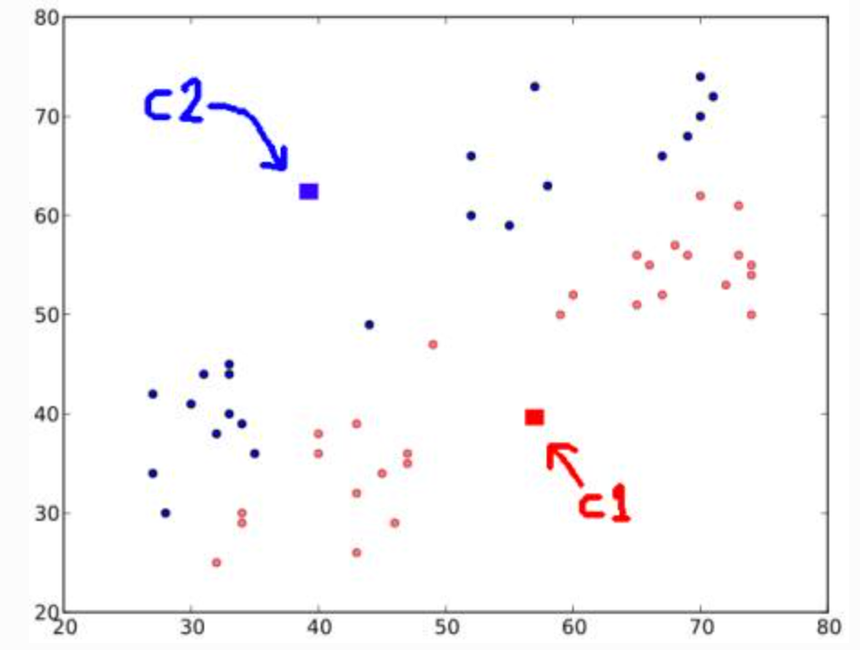
Randomly choose 2 centroids, C1C_1C1​﻿ and C2C_2C2​﻿​

Calculate distance for each from both centroid. Closer to C1C_1C1​﻿ are labeled 000﻿, o.w labeled 111﻿​

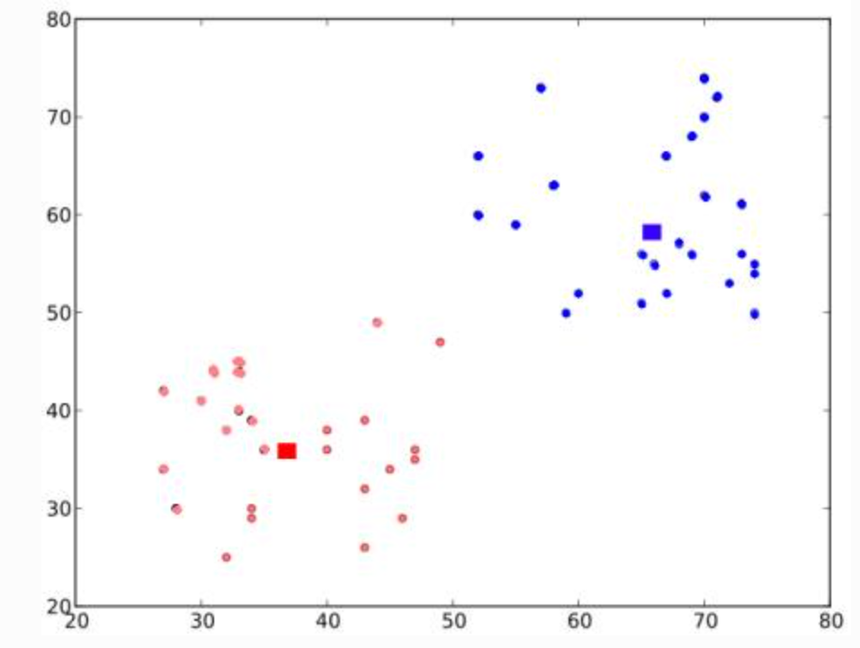
Next, compute the average for blue and red points and update the centroids

Iterate over 2 and 3 until convergence (or stopping criteria on number of iteration, or precision) is reach

The distances between test data and their centroids are minimum

min  [J=∑redsd(C1,red)+∑bluesd(C2,blue)]min \;[J=\sum_{reds}d(C_1, red)+\sum_{blues}d(C_2, blue)]min[J=∑reds​d(C1​,red)+∑blues​d(C2​,blue)]﻿​

full script

Python

Copy

import numpy as np
import cv2

img = cv2.imread('home.jpg')
Z = img.reshape((-1,3))
# convert to np.float32
Z = np.float32(Z)
# define criteria, number of clusters(K) and apply kmeans()
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 10, 1.0)
K = 8
ret, label, center = cv2.kmeans(
	Z, K, None, criteria, 10, cv2.KMEANS_RANDOM_CENTERS
)
# Now convert back into uint8, and make original image
center = np.uint8(center)
res = center[label.flatten()]
res2 = res.reshape((img.shape))

cv2.imshow('res2',res2)
cv2.waitKey(0)
cv2.destroyAllWindows()