5.3 Frequentist decision theory

In frequentist decision theory, we don’t use prior and thus no posterior, so we can’t define the risk as the posterior expected loss anymore.

5.3.1 Computing the risk of an estimator

The frequentist risk of an estimator $\pi$, applied to data $x$ sampled from the likelihood $p(x|\theta)$:

Exemple

We estimate the true mean of a Gaussian. Let $x_n \sim \mathcal{N}(\theta^*,\sigma^2=1)$. We use a quadratic loss, so the risk is the MSE.

We compute the risk for different estimators, the MSE can be decomposed:

with $bias(\hat{\theta})=\mathbb{E}[\hat{\theta}-\theta^*]$.

• $\pi_1=\bar{x}$ is the sample mean. This is unbiased, so its risk is:

• $\pi_2=\mathrm{median}(\mathcal{D})$. This is also unbiased. One can show its variance is approximately:

• $\pi_3$ returns the constant $\theta_0$ so its biased is $(\theta_0-\theta^*)$, and its variance is zero. Hence:

• $\pi_\kappa$ is the posterior mean under a $\mathcal{N}(\theta|\theta_0,\sigma^2/\kappa)$ prior:

We can derive its MSE as follow:

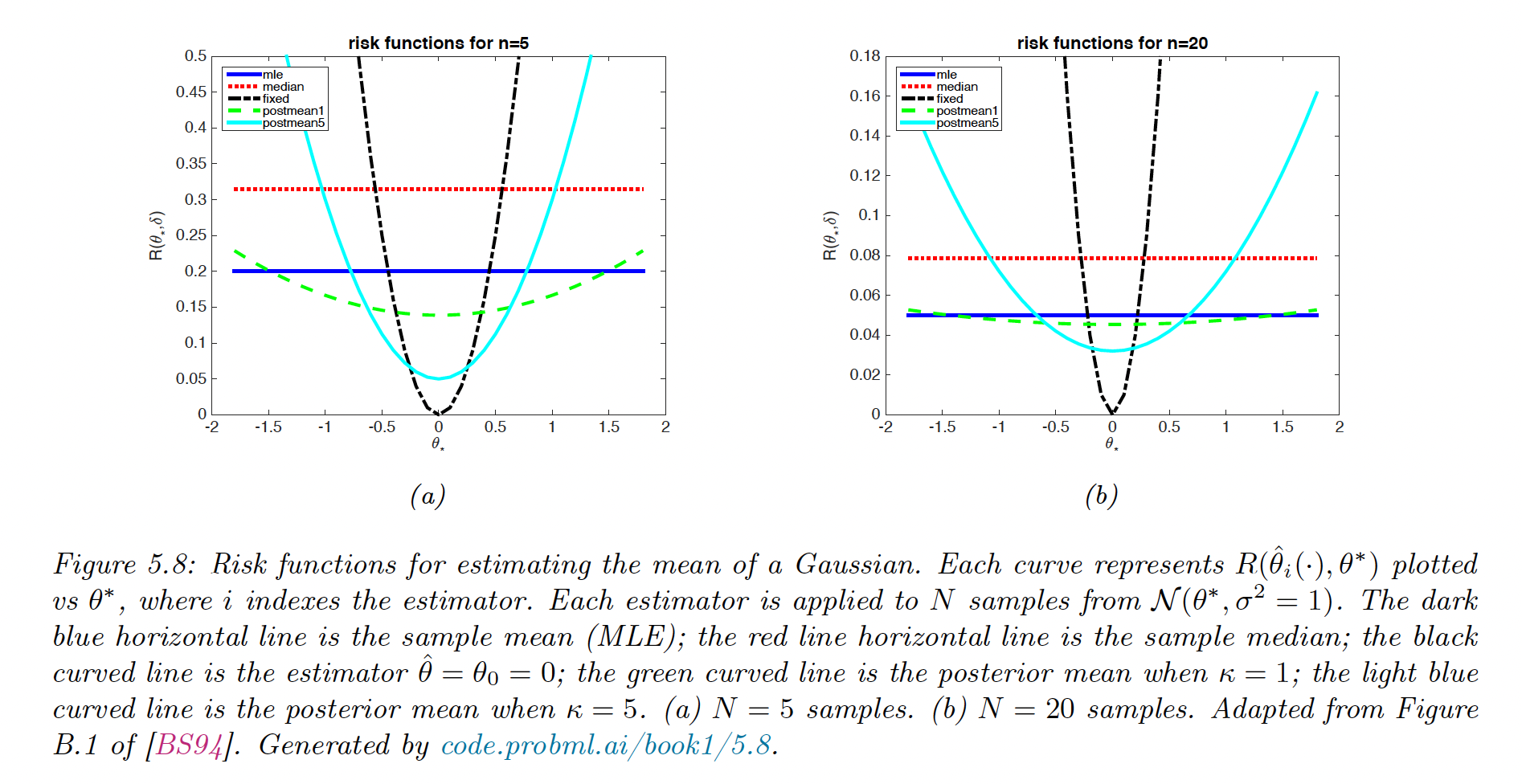
The best estimator depends on $\theta^*$, which is unknown. If $\theta_0$ is far from $\theta^*$, the MLE is best.

Bayes risk

In general the true distribution of $\theta$ is unknown, so we can’t compute $R(\theta,\pi)$. One solution is to average out all values of the prior $\pi_0$ for $\theta$. This is the Bayes risk or integrated risk.

The Bayes estimator minimizes the Bayes risk:

which corresponds to optimal policy recommended by Bayesian decision theory here.

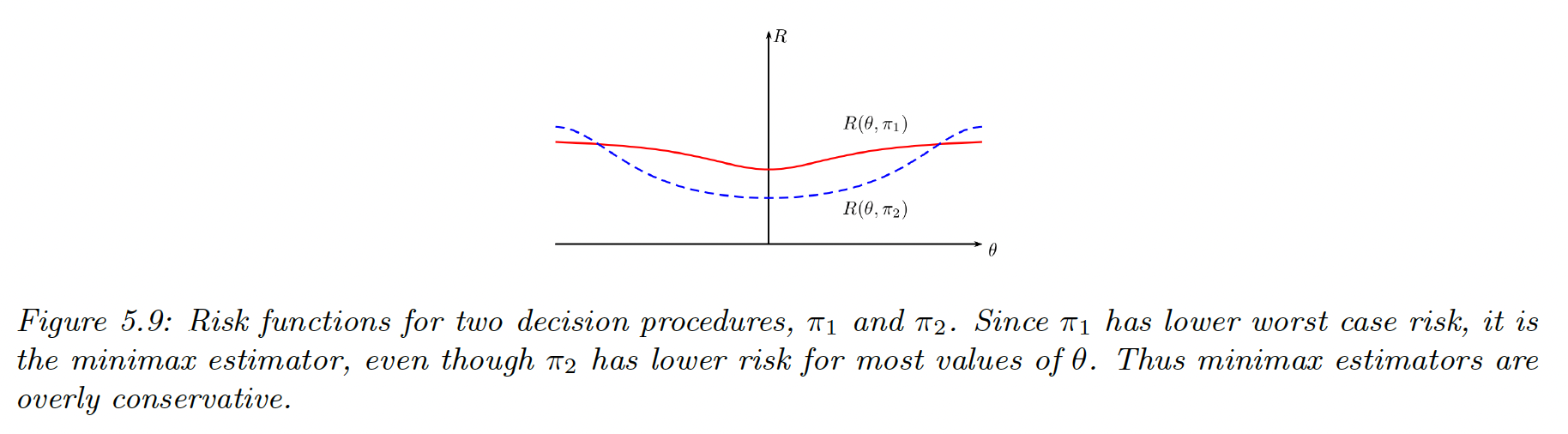
Maximum risk

To avoid using a prior in frequentist, we can define the maximum risk:

To minimize the maximum risk, we use minimax $\pi_{MM}$. Computing them can be hard though.

5.3.2 Consistent estimators

An estimator $\pi: \mathcal{X}^N\rightarrow\Theta$ is consistent when $\hat{\theta}(\mathcal{D}) \rightarrow \theta^*$ as $N\rightarrow +\infin$, where the arrow is the convergence in probability.

This is equivalent to minimizing the 0-1 loss $\mathcal{L}(\hat{\theta},\theta^*)= \mathbb{I}(\hat{\theta}\neq \theta^*)$.

An example of consistent estimator is the MLE.

Note that an estimator can be unbiased but not consistent, like $\pi(\{x_1,...,x_N\})=x_N$. Since $\mathbb{E}[\pi(\mathcal{D})]=\mathbb{E}[x]$ this is unbiased, but the sampling distribution of $\pi(\mathcal{D})$ doesn’t converge to a fix value so it is not consistent.

In practice, it is more useful to find some estimators that minimize the discrepancy between our empirical distribution $p_\mathcal{D}(x|\mathcal{D})$ and the estimated distribution $p(x|\hat{\theta})$. If this discrepancy is the KL divergence, our estimator is the MLE.

5.3.3 Admissible estimators

$\pi_1$ dominates $\pi_2$ if:

An estimator is admissible when it is not dominated by any others.

In figure 5.8 above, we see that the risk of the sample median $\pi_2$ is dominated by the sample mean $\pi_1$.

However this concept of admissibility is of limited value, since $\pi_3(x)=\theta_0$ is admissible even though this doesn’t even look at the data.