Proba ML
7. Linear Algebra
7.2 Matrix Multiplication

7.2 Matrix multiplication

The product of A∈Rm×nA\in\mathbb{R}^{m \times n} and B∈Rn×pB\in\mathbb{R}^{n \times p} is AB=CAB=C with:

Cij=∑k=1nAikBkjC_{ij}=\sum_{k=1}^n A_{ik}B_{kj}

Note that the number of columns of AA must match the number of rows of BB.

Matrix multiplication complexity averages O(mnp)O(mnp), faster methods exists (like BLAS) and hardware parallelizing the computation, like TPU or GPU.

  • Matrix multiplication is associative: A(BC)=(AB)CA(BC)=(AB)C
  • Matrix multiplication is distributive: A(B+C)=AB+BCA(B+C)=AB+BC
  • In general, it is not commutative: AB≠BAAB\neq BA

7.2.1 Vector-vector products

Inner product

Given two vectors x,y∈Rn\bold{x}, \bold{y}\in\mathbb{R}^n, their size is (n,1)(n,1) . The inner product is the scalar:

⟨x,y⟩=x⊤y=∑i=1nxiyi\lang\bold{x},\bold{y}\rang=\bold{x}^\top \bold{y}=\sum_{i=1}^n x_iy_i

Note that x⊤y=y⊤x\bold{x}^\top\bold{y}=\bold{y}^\top\bold{x}

Outer product

Given two vectors x∈Rn\bold{x}\in \mathbb{R}^n and y∈Rm\bold{y}\in \mathbb{R}^m (they no longer have the same size), the outer product is a matrix Rn×m\mathbb{R}^{n\times m}:

xy⊤=[x1y1…x1ym⋮⋱⋮xny1…xnym]\bold{x}\bold{y}^\top=\begin{bmatrix}x_1y_1 & \dots & x_1y_m \\ \vdots &\ddots & \vdots \\ x_n y_1 & \dots & x_n y_m\end{bmatrix}

7.2.2 Vector-matrix products

Given matrix A∈Rm×nA\in\mathbb{R}^{m\times n} and x∈Rn\bold{x} \in \mathbb{R}^{n}, the product is y=Ax∈Rm\bold{y}=A\bold{x} \in \mathbb{R}^m

This can be viewed as inner product on rows:

y=[a1⊤x⋮am⊤x]\bold{y}=\begin{bmatrix} a_1^\top \bold{x}\\ \vdots \\ a_m^\top\bold{x}\end{bmatrix}

Or linear combination on columns:

y=[∣a1∣]x1+⋯+[∣an∣]xn\bold{y}= \begin{bmatrix}| \\a_1\\|\end{bmatrix}x_1+\dots+\begin{bmatrix}| \\a_n\\|\end{bmatrix}x_n

In this latter view, A is a set of basis vectors defining a linear subspace.

7.2.3 Matrix-matrix products

The main view is a inner product between row vectors of AA and columns vectors of BB:

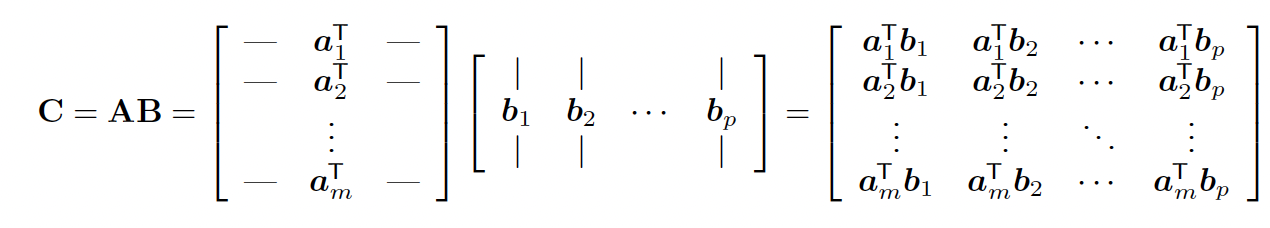
Screen Shot 2023-02-24 at 09.06.04.png

If A∈Rn×mA\in\mathbb{R}^{n\times m} and B∈Rm×dB\in\mathbb{R}^{m\times d}, then C∈Rn×dC\in\mathbb{R}^{n\times d}

7.2.4 Matrix manipulations

Summing slices

Let X∈Rn×dX\in\mathbb{R}^{n\times d}, we can average rows of XX by pre-multiplying a vector of ones:

xˉ⊤=1N1N⊤X=[∑i=1nxi1…∑i=1nxid]\bar{\bold{x}}^\top=\frac{1}{N}\bold{1}_N^\top X= \begin{bmatrix}\sum_{i=1}^n x_{i1}&\dots & \sum_{i=1}^nx_{id}\end{bmatrix}

Conversely, we can average columns by post-multiplying.

Hence, the overall mean is given by:

xˉ=1ND1N⊤X1D\bar{x}=\frac{1}{ND}\bold{1}_N^\top X \bold{1}_D

Scaling

If we pre-multiply XX by a diagonal matrix SS, we scale each row by sis_i:

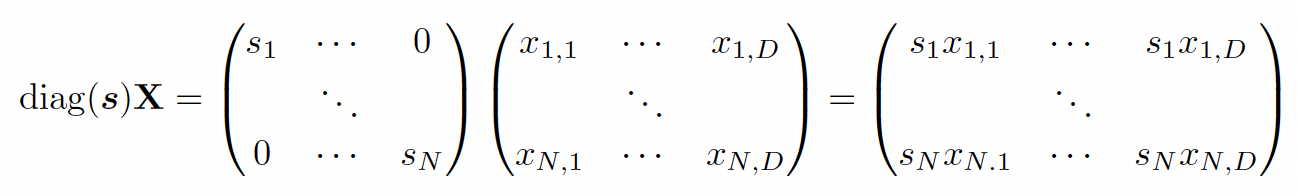
Screen Shot 2023-02-24 at 09.21.55.png

Conversely, we scale columns by post-multiplying XX with the diagonal matrix SS

Therefore, the normalization operation can be written:

Xstd=(X−1Nμ⊤)diag(σ)−1X^{std}=(X-\bold{1}_N\mu^\top)\mathrm{diag}(\sigma)^{-1}

where μ\mu is the empirical mean vector and σ\sigma the empirical standard deviation vector.

Scatter matrix

The sum of squares matrix S0∈RD×DS_0\in\mathbb{R}^{D\times D} is:

S0≜X⊤X=∑i=1Nxixi⊤S_0\triangleq X^\top X=\sum_{i=1}^Nx_ix_i^\top

The scatter matrix Sxˉ∈RD×DS_{\bar{x}}\in\mathbb{R}^{D\times D} is:

Sxˉ≜∑i=1N(xi−xˉ)(xi−xˉ)⊤=∑i=1Nxixi⊤−Nxˉxˉ⊤S_{\bar{x}}\triangleq\sum_{i=1}^N(x_i-\bar{x})(x_i-\bar{x})^\top=\sum_{i=1}^N x_i x_i^\top-N\bar{x}\bar{x}^\top

The Gram matrix K∈RN×NK\in\mathbb{R}^{N\times N} is:

K≜XX⊤K\triangleq XX^\top

The square pairwise distance between X∈Rm×dX\in \mathbb{R}^{m\times d} and Y∈Rn×dY\in\mathbb{R}^{n \times d} is:

Dij=∣∣xi−yj∣∣22=(xi−yj)⊤(xi−yj)=∣∣xi∣∣22−2xi⊤yj+∣∣yj∣∣22D_{ij}=||x_i-y_j||^2_2=(x_i-y_j)^\top(x_i-y_j)=||x_i||^2_2-2x_i^\top y_j+||y_j||^2_2

This can also we written as:

D=x^1m−2XY⊤+1ny^D= \hat{x}\bold{1}_m-2XY^\top+\bold{1}_n\hat{y}

where x^=diag(XX⊤)\hat{x}=diag(XX^\top)

7.2.5 Kronecker products

A∈Rm×nA\in\mathbb{R}^{m\times n} and B∈Rp×qB\in\mathbb{R}^{p\times q}, then the Kronecker product belongs to Rmp×nq\mathbb{R}^{mp\times nq}:

A⊗B=[a11B…a1nB⋮⋱⋮am1B…amnB]A \otimes B= \begin{bmatrix} a_{11}B & \dots & a_{1n}B \\ \vdots & \ddots & \vdots \\ a_{m1}B & \dots & a_{mn}B \end{bmatrix}

Some useful properties:

(A⊗B)—1=A−1⊗B−1(A\otimes B)^{—1}=A^{-1}\otimes B^{-1}

(A⊗B)vec(C)=vec(BCA⊤)(A \otimes B)\mathrm{vec}(C)=\mathrm{vec}(BCA^\top)

7.2.6 Einstein summation

Einsum consists in removing the ∑\sum operator for matrix and tensor products:

Cij=∑kAikBkj⇒AikBkjC_{ij}=\sum_k A_{ik}B_{kj} \Rightarrow A_{ik}B_{kj}

And for more complex operations:

Lnc=∑d∑k∑tSntkWkdVdc⇒SntkWkdVdcL_{nc}=\sum_d\sum_k\sum_t S_{ntk}W_{kd}V_{dc} \Rightarrow S_{ntk}W_{kd}V_{dc}

Einsum can perform computations in an optimal order, minimizing time and memory allocation.

7.1 Intro7.3 Matrix Inversion